[풀이]
ps를 한창하던 2018년, 여름 즈음에 이 문제를 봤던 기억이 있다. 다른 알고리즘에 비해서 dp는 너무 어렵게 느껴져서, 풀다가 포기했던 기억이 난다.
아마 같이 문제를 봤던 형님은 얼마 안 가 풀었는데, 답지를 보자니 dp는 답지보면 너무 쉽게 느껴져서 다음에 풀어보기로 하고 군 입대를 했다....
잡설은 뒤로하고, tree에서 dp를 쓰는 특이한 문제로 기억된다.
자, dp table $dp[i][j]$를
$j$가 0일 경우 => $i$번째 node가 얼리어답터가 아닐 때 $i$의 subtree를 완성시키는데(모두 수용하도록 하는데에) 필요한 최소 얼리어답터 수
$j$가 1일 경우 => $i$번째 node가 얼리어답터일 때 $i$의 subtree를 완성시키는데필요한 최소 얼리어답터 수
로 정의하자.
왜 이렇게 정의 했냐면, $i$가 얼리 어답터일 때 $i$의 subtree를 완성시키는데 필요한 최소 얼리어답터를 구하는 점화식 과 $i$가 얼리가 아닐때 완성시키는데 필요한 최소 얼리를 구하는 점화식이 다르다.
왜 다르냐면... 아래설명을 보면 알게 된다.

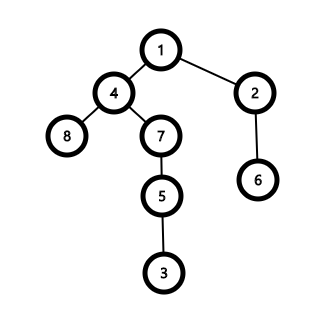
자, 이런 tree가 있을때 dp table의 정의대로 한번 채워나가보자.
먼저, leaf node인 $3, 8, 9$를 보면 $dp[3][0] = dp[8][0] = dp[9][0]= 0$, $dp[3][1] = dp[8][1] = dp[9][1]= 1$이다.
$dp[3][0]$의 값을 생각하는게 까다로운데, dp table의 정의에 따라 이런 경우는 생기지 않으므로 undefined의 의미로 0을 주었고, 이 편이 다음 계산이 편해진다.

자, 이제 각 leaf node의 바로 위 node들 $2, 4, 5$를 채워보자.
$dp[2][0]$은 정의에 따라 $2$가 얼리어답터가 아닐때 $2, 6$이 모두 수용해야 하므로 $6$이 얼리어답터가 되어야한다. 따라서, $dp[6][1]$의 값인 1이 $dp[2][0]$의 값이다.
$dp[2][1]$은 정의에 따라 $2$가 얼리어답터일 때 $2, 6$이 모두 수용해야 하므로 $6$이 얼리어답터이든 아니든 알바가 아니다. 따라서, $min(dp[6][0], dp[6][1]) + 1$인 1이 $dp[2][1]$의 값이다.
$dp[5][j]$도 같은 방식으로, 같은 값을 갖는다.

$dp[4][j]$를 채우려면 $dp[7][j]$값이 필요하니 $dp[7][j]$부터 구해보자.
$dp[7][0]$은 정의에따라 $7$은 얼리어답터가 아니면서 수용해야하므로 $5$가 반드시 얼리어답터여야한다. 따라서, $dp[7][0]$의 값은 $dp[5][0]$의 값인 1이다.
$dp[7][1]$은 정의에따라 $7$이 얼리어답터이므로 자식인 $5$가 얼리어답터이든 아니든 알바가 아니다.
왜냐면, dp table을 정의할 때 그 node의 subtree가 이미 모두 수용되는 상태라고 정의했기 때문이다.
따라서, $dp[7][1]$은 $min(dp[5][0], dp[5][1]) + 1 $인 2가 $dp[7][1]$의 값이다.

$dp[4][j]$을 보자. child가 2개다.
$dp[4][0]$은 $4$가 얼리어답터가 아니면서 수용해야한다. 그런 경우는 자식인 $7, 8$이 얼리어답터인 경우 밖에 없다. 따라서, $dp[4][0]$은 $dp[8][1] + dp[7][1]$인 1이다.
$dp[4][1]$은 $4$가 얼리어답터면서 수용해야한다. 마찬가지로, 이런 경우 자식인 $7, 8$이 얼리어답터이든 아니든 알바가 아니다. 이미 그 subtree는 수용하고 있는 상태니까. (왜? dp table을 그렇게 정의해서)
따라서, $dp[4][1]$은 $min(dp[7][0], dp[7][1]) + min(dp[8][0], dp[8][1]) + 1 $인 2이다.
같은 방식으로 마지막 root node인 $1$의 dp table을 찾아보면 $dp[1][0] = 3, dp[1][1] = 3$이다. 둘 중 작은 값이 정답이므로 3이 정답이다.
정리해보면,
$dp[i][0] = \sum_{child} dp[child][1]$
$dp[i][1] = \sum_{child} min(dp[child][0], dp[child[1])$ + 1
이다.
한 가지, 문제를 풀면서 주의해야 할 점은 tree의 root를 모른다. 게다가 undirected이므로 사실 tree가 아니다.
따라서, undirected로 연결해주되, 아무 한 점을 root로 잡고 dp를 돌리면서 parent의 dp테이블에는 접근하지 않도록 해주는게 핵심인 듯 하다.
[코드] -- 추가바람