[문제]
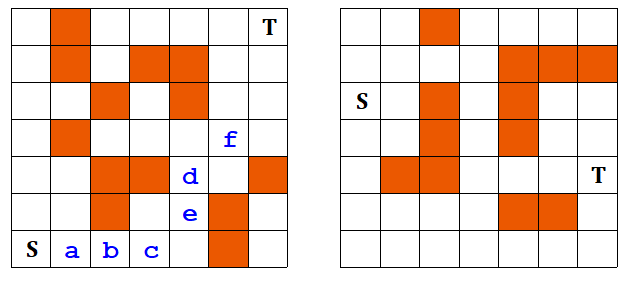
어떤 도시에서 코로나-19사태에 대응하여 지점 S에서 지점 T로의 이동을 완전히 봉쇄하려고 한다. 아래 그림에서 색으로 칠해진 부분은 사람이 이동할 수 없는 공간(산이나 호수, 강)이다. 여러분의 목표는 단 하나의 그리드 위치(Cell)에 장애물을 세워 S에서 T로 갈 수 있는 경로(path)를 막는 것이다. 왼쪽 예시의 경우 {a, b, c, d, e, f}로 표시된 곳 중 하나를 막으면 S에서 T로의 이동을 완전히 봉쇄할 수 있다. 오른쪽 예시의 경우 하나의 Cell만을 막아서는 S에서 T로 가는 것을 막을 수 없다. 여러분은 S-T 경로를 봉쇄할 수 있는 Cell을 모두 찾아 그 index를 사전식으로 나열해야 한다(S나 T를 직접 막을 수는 없다). 만약 봉쇄할 수 없을 때는 0을 출력한다. 단, 사람들의 이동은 상하좌우 4방향으로만 가능하며 대각선 방향으로는 불가능하다.
[입출력]
lock.inp의 첫 줄에 도시 공간의 차원 $n \times m$을 나타내는 두 정수 $n, m$이 주어진다. 각각은 $5 \leq n,m \leq 30$이다. 이어지는 $n$개의 줄에 길이 $m$인 문자열이 주어진다. 문자열에서 ‘#’은 장애물, ‘_’(underbar)는 이동 가능한 공간을 나타낸다. S와 T의 위치는 대문자 S,T로 표시된다. 첫 줄에 block cell의 개수 $k$를 출력하고 이어 각 cell의 좌표 $(x,y)$의 $x y$값을 사전식으로 출력한다. 단, 왼쪽 아래점의 좌표는 (1,1)이다. 처음부터 S-T가 단절되어 있어도 $k = 0$이 된다.

[풀이]O($n^2m^2$)
시험기간이라고 간단한 문제를 내주신듯 하다. $n,m$이 매우 작으므로 모든 각 공간을 하나씩 봉쇄하여 bfs를 돌리면 해결 가능하다.
dfs 1번으로 단절점을 찾는 문제인 줄 알고 그렇게 풀려고 했으나, 단절점을 끊어낸 뒤 S 와 T가 다른 component의 집합인지 판단하는 과정이 결국 dfs나 bfs를 돌려야 하므로 시간복잡도는 동일하다. 물론 2by2행렬의 모든 점이 단절점이 되는 경우는 절대 없으므로 O($nm*max(n,m)$)에 수렴할 것으로 예상되나 크게 의미있는 시간차이를 보여주지는 않을 것이므로 구현하지는 않았다.
나는 똥멍청이다. 단절점을 찾는 dfs를 돌면서 S T와 연결 된 정점인지 체크가 바로 가능하다. dfs를 재귀호출하면서 S와 연결되어 있는지 체크 가능하고, dfs return할 때 flag를 주어서 T와 연결 된 정점인지 체크할 수 있다.
dfs의 결과가 트리이니, 트리의 모든 단절점 중 S T 모두에게 연결된 정점만 문제에서 요구하는 단절점이 된다.
당연히 dfs 1번으로 처리되니 O($nm$)에 처리된다.
